What are Vectors and Why Store Them in a Vector Database?
With the rise of large language models (LLMs) like GPT, you probably noticed the increased demand for vector databases. They are praised as “infinite memory for LLMs,” but what that means might not be clear to everyone.
If you’re a bit confused about why you might need yet another database for your next project if you want to include an LLM or generally need a refresher in vectors, then this is the right article for you. It will explain vectors and vector databases, and illustrate their usage with practical examples.
What is a Vector?
A vector is a geometrical object that has a length and a direction. It starts at one point and ends at another. Figure 1 illustrates a 2D vector going from point A to point B.
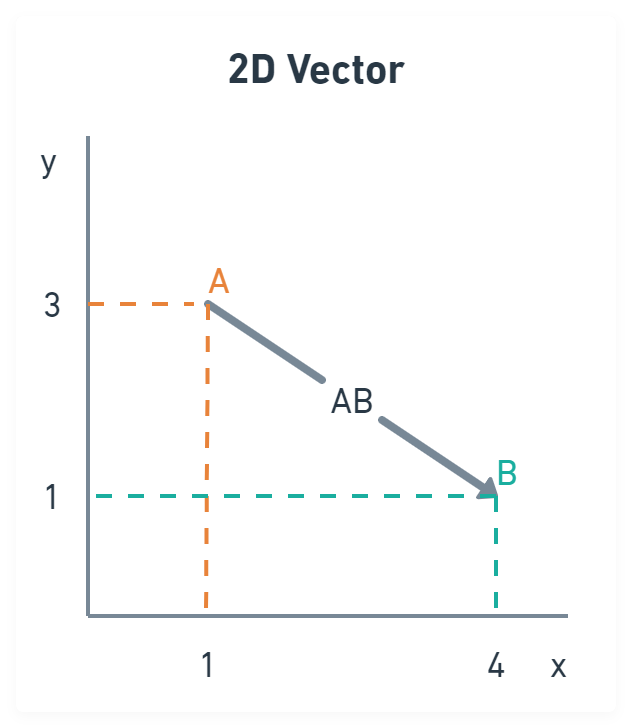 Figure 1: 2D vector
Figure 1: 2D vector
As you can see, the vector has a direction from A (1,3) to B (4,1). It also has a length but is not explicitly defined; we must calculate it. We can use the hypotenuse formula for this, just like in school.
a = 3 - 1 = 2
b = 4 - 1 = 3
a² + b² = c²
2² + 3² = 4 + 9 = 13 = c²
3.61 ~= c
So, the length of our vector is around 3.61.
While this small exercise might seem boring, it illustrates an important property of vectors: They come with a mathematical foundation called vector algebra that allows us to analyze them precisely. Just what we need when writing software with it!
If we know how to calculate the relations between points through vectors, we can use this to model (hint hint) all kinds of things from the real world in our software.
How are Vectors Represented in Code?
There are several ways to represent a vector in code. We could save it as an object like this:
const v = {
startX: 1,
startY: 3,
endX: 4,
endY: 1
}However, since the interesting part of a vector is its length and direction (i.e., when rendering a pixel, we want to know where to display it, not how far it's away from other pixels), we can omit some parts. If we move all vectors to (0,0), we don’t have to save that point, as it’s always the same.
In Figure 2, you see that a moved vector, also known as a translated vector, has the same direction and length but starts in a different place.
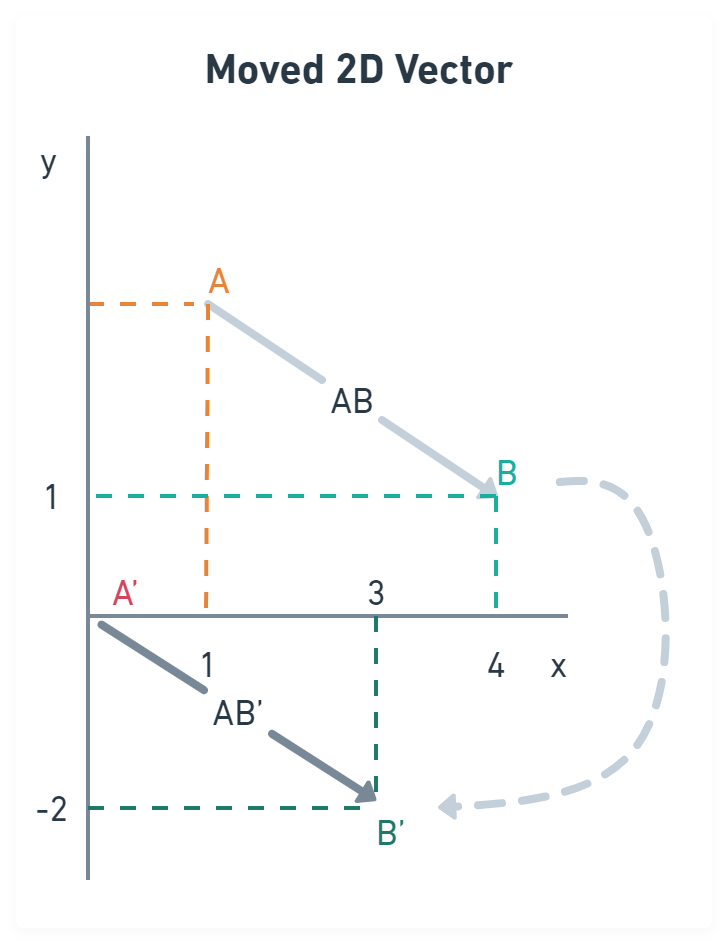 Figure 2: Moved 2D vector
Figure 2: Moved 2D vector
In our case, that place is the point (0,0), so we can omit it in our
representation. This leaves us with endX and endY; since they always come in
the same order, we can put them in an array of size two.
const v = [3,-2]If you see a vector represented like this, you can assume it starts at the
center of the coordination system. For example, a 3D vector [4,2,5] would
begin with [0,0,0] even if it has more dimensions than two.
This brings us to the next important property of vectors: they can have an arbitrary number of dimensions. While only two or three dimensions make sense in visual applications, there are other applications, like recommendation engines or LLMs, where many more dimensions are useful.
More than three dimensions might sound abstract, but it makes more sense to imagine a dimension less like a geometrical direction and more like a characteristic. Take a T-shirt, for example. It has a color, a size, a price, a material, etc. Despite more than three properties, each could be represented as a vector dimension.
Practical Examples of Vectors
There are many different applications of vectors in software development, some more obvious than others.
Computer Graphics
The most obvious example is using 2D vectors to represent pixels on a screen.
[752,330]
If you used HTML and CSS, you might have encountered 3D vectors in 2D visualizations. Here, the third dimension is the z-index, which decides which element is rendered last and will hide all other elements with a lower z-index. The vectors are part of the CSS properties of each HTML element.
{x:723,y:544,z-index:99}
Applications like video games use three dimensions to represent points in a 3D space.
[923,123,33]
In fact, they often use four dimensions since they make some common 3D calculations easier. These applications have to transfer the 3D points to the 2D pixels of your screen to display them, which is called projection.
Recommendation Engines
A more advanced example of vector usage is a recommendation engine. Here, the dimensions are the properties of items. This could be wares like clothes and social media posts or videos. This example has nothing to do with visual representations, so there can be more than three dimensions. Nevertheless, as all vectors adhere to the rules of vector algebra, we can use them to do meaningful calculations with them.
You could represent a movie with a vector that contains its length, resolution, and release date—all numbers, so it’s not too complicated.
The following vector represents a ninety-minute movie with full-HD resolution from 2010:
[5400,1080,1265538522]
When a user watches the movie, you can save the corresponding vector. After saving a reasonable amount, you can calculate a vector representing the user's movie preference.
When you need to recommend movies in the future, you can compare the user's preference vector to a movie vector and list the closest movies. The user may only watch short movies or prefer movies from a certain time in the past.
Machine Learning
You might have noticed that recommending movies based on their length and release dates probably won’t yield the best results. That’s where machine learning (ML) comes into play.
With ML, you teach an algorithm to categorize different items, which essentially means assigning vectors to them automatically. This is helpful since it’s often hard to decide how many dimensions a vector should have, let alone what values each dimension needs. Such a system can analyze an image and assign a huge vector that could encode information like how many people are in this image, what type of clothes they are wearing, and which painting style was used to create it, etc.
In the case of an LLM, a system has to learn how to form reasonable sentences by assigning each word a vector that encodes where it can use the word. This could require hundreds or thousands of dimensions, so it wouldn’t be feasible for humans to do it manually.
Now that you understand what vectors are and their use cases in different types of software, let’s look at vector databases.
What’s a Vector Database?
A vector database is optimized for storing and querying vectors and their related metadata.
Each database has a different, unique selling point. MySQL helps with data deduplication, Redis is for high-performance data retrieval, and ElasticSearch enables your app to do full-text searches.
Vector databases like Upstash Vector let you query records via approximate nearest neighbor (ANN) algorithms. As discussed above, you have a vector and want a list of vectors that are in some way related to it. Think of it a bit like ElasticSearch, but instead of using different text storage and search methods, it uses vector algebra.
A record's metadata in a vector database usually contains information related to that vector. For example, if you have a vector for an image, the metadata could include a URL to that image.
How to Query a Vector Database?
Vector databases offer different ANN algorithms to query the data. As the approximate part of ANN implies, this isn’t a 100% accurate way to get the nearest neighbor, but the alternative is a full table scan for each query, which is unfeasible in practice. Upstash Vector uses DiskANN to query indexes directly from SSD and enhances it with FreshDiskANN for memory access of recently changed data.
You must choose a vector similarity function when creating an index for a vector database. Upstash Vector offers three of them. Let’s check them out!
Euclidean Distance
Euclidean distance is the easiest function. It simply measures the distance between two vectors.
It is useful in cases where you want to know how close the end point of a vector
is to another one. [1,1] and [10000,10000] have the same direction, but
they aren’t close to each other. For example, in a 2D game, you might only load
vectors close to a player entity but nothing outside their viewport to improve
performance.
Cosine Similarity
The result of the cosine similarity function doesn’t measure the distance between two vectors but the difference in their direction.
It is useful for recommendation engines that operate on many dimensions. Let’s take the movie recommendation again as an example.
If we have 3 genres, action, comedy, and drama, the vectors representing each movie would have 3 dimensions.
- An action movie vector looks like this
[1,0,0] - A comedy movie vector looks like this
[0,1,0] - A drama movie vector looks like this
[0,0,1]
If a user watches 8 comedies and 2 dramas, their preference vector looks like
this [0,8,2].
As we don’t expect movies with values other than 1 and 0, there can’t be a comedy movie that is “more comedy” (i.e., a comedy value bigger than 1) than another comedy movie. It’s enough to check if the movie vector points in a similar direction as the preference vector; we don’t need to check how “far into that direction” it points.
Cosine similarity will return values between 1 and -1, depending on how well the vector directions align. This is the case if the user watched 10 or 1000 movies.
Dot Product
The dot product will include length and direction in the calculation. Meaning, vectors aren’t just similar when they point in the same direction, but also when they have a similar length.
In our previous recommendation engine example, we only allowed movies to have 1 or 0 values. While it’s a matter of personal taste if one comedy movie is funnier than another, there are reasonable use cases where the magnitude of a dimension might be crucial.
We could include an additional runtime dimension for the length of a movie.
[0,1,0,70]
[0,1,0,120]
[0,0,1,200]
However, as there aren’t any movies with negative runtime, this dimension would always point in the same direction, independently of the movie length, so cosine similarity wouldn’t work since it ignores the vector length. The dot product is the better choice that allows us to consider the magnitude in addition to the direction.
What Do Vector Databases Bring to LLMs?
LLMs have an input and output limit. You can’t simply put in a question about a book and the whole book at once to get an answer. A vector database allows you to store the book in easily digestible parts for an LLM.
This works by splitting the book up, converting it into a text embedding (i.e., encoding some text as a very big vector), and storing it into a vector database. The conversion into an embedding can be done with special embedding models, which work similarly to regular LLMs, just that they will give you a huge vector as an answer.
When you want to ask a question about the book via LLM, you also convert the question to a text embedding, use it to search the database for related vectors from the book, and send the question embedding together with the found book embeddings to your LLM.
This way, you would only have to feed your LLM parts of the book with each query and not the whole thing.
This isn’t the most accurate way of solving this issue, but the alternatives would be to train or fine-tune an LLM with your book, which takes considerably more effort. Sometimes, it isn’t even possible since training requires huge amounts of data you don’t have.
Now that you understand why you need a vector database, we should check why you would use Upstash Vector.
Why Upstash Vector?
The most crucial selling point of Upstash Vector is its serverless architecture, which means you just pay for what you use, and 10k daily queries and the first 1GB of storage are free! Upstash Vector uses DiskANN and FreshDiskANN, so you get low query latency at a very low price. $0.4 per 100k requests and $0.25 per 1GB. This way, your database scales with you in performance and costs.
Upstash Vector also supports the three mentioned similarity functions, Euclidean Distance, Cosine Similarity, and Dot Product, and comes with SDKs for TypeScript and Python and a REST API.
Summary
Software developers have used vectors in any application for over half a century, and they have good reasons for it. Vector algebra is a versatile math tool that allows us to model the real world, from geometrical spaces to texts.
Now that everyone wants to add AI to their products, they need efficient ways, especially solutions to the input limitations LLMs pose. Only some people have the time, money, or data to train or fine-tune an LLM.
That’s where databases like Upstash Vector come into play. So, if you want to build something that matters without breaking the bank, check it out!
